Estoy con el coche en un atasco durante un día lluvioso. Fruto de la desesperación, me empiezo a preguntar si es verdad que hay más atascos durante los días de lluvia. Durante un largo periodo de tiempo voy apuntando la información de cada día en una tabla.
| Lluvia | Sin lluvia | |
| Atasco | 13% | 22% |
| Sin atasco | 11% | 54% |
Gracias a esta tabla puedo ver que la probabilidad de que un día llueva y haya atasco es de un $13\% = 0,13$. Como era de esperar, la suma de todas las casillas es $100\%$.
En la tabla tengo información de las dos variables (atasco y lluvia) mezcladas. Entonces, ¿cómo puedo calcular la probabilidad de que un día haya atasco?
Pues simplemente tengo que sumar los días con atasco y lluvia ($13\%$) con los días con atasco sin lluvia ($22\%$). Es decir, me es indiferente si llueve o no, por lo que consideramos ambos casos. De esta forma, obtengo información de una única variable a través de información de las dos variables mezcladas. De hecho, podemos sumar las filas y columnas de nuestra tabla para recopilar toda esta información.
| Lluvia | Sin lluvia | TOTAL | |
| Atasco | 13% | 22% | 35% |
| Sin atasco | 11% | 54% | 65% |
| TOTAL | 24% | 76% | 100% |
Ahora podemos ver más fácilmente que, por ejemplo, hay una probabilidad de un $24\%$ de que llueva o de un $65\%$ de que no haya atasco. La probabilidad que representa cada casilla de la tabla es la siguiente:
| Lluvia | Sin lluvia | TOTAL | |
| Atasco | $P(\textrm{Atasco} \cap \textrm{Lluvia})$ | $P(\textrm{Atasco} \cap \overline{\textrm{Lluvia}})$ | $P(\textrm{Atasco})$ |
| Sin atasco | $P(\overline{\textrm{Atasco}} \cap \textrm{Lluvia})$ | $P(\overline{\textrm{Atasco}} \cap \overline{\textrm{Lluvia}})$ | $P(\overline{\textrm{Atasco}})$ |
| TOTAL | $P(\textrm{Lluvia})$ | $P(\overline{\textrm{Lluvia}})$ | 1 |
Sabemos que hay atasco ($\textrm{Atasco}$) si hay atasco y lluvia ($\textrm{Atasco} \cap \textrm{Lluvia}$) o si hay atasco pero no llueve ($\textrm{Atasco} \cap \overline{\textrm{Lluvia}}$).
$$P(\textrm{Atasco}) = P(\textrm{Atasco} \cap \textrm{Lluvia}) + P(\textrm{Atasco} \cap \overline{\textrm{Lluvia}})$$
De forma general, tenemos:
$$P(A) = P(A \cap B) + P(A \cap \overline{B})$$
Si queremos calcular la probabilidad de que se cumpla un suceso $A$, podemos desglosarla en casos según lo que suceda en otra variable $B$.
En vez de considerar si llueve o no, también podemos recoger los datos según los días de la semana. Podemos crear una tabla tal que así:
| Entre diario | Sábado | Domingo | TOTAL | |
| Atasco | 25% | 4% | 6% | 35% |
| Sin atasco | 47% | 10% | 8% | 65% |
| TOTAL | 72% | 14% | 14% | 100% |
De esta forma, la probabilidad de que haya un atasco se puede desglosar en que haya un atasco entre semana, que lo haya un sábado y que lo haya un domingo.
$$P(\textrm{Atasco}) = P(\textrm{Atasco} \cap \textrm{Diario}) + P(\textrm{Atasco} \cap \textrm{Sáb.}) + P(\textrm{Atasco} \cap \textrm{Dom.})$$
De forma general, si tenemos una variable $B$ que puede desglosarse en varias opciones disjuntas (no puede ser entre diario y sábado a la vez), podemos utilizarla para desglosar la probabilidad de $A$ en varios casos.
$$P(A) = P(A \cap B_1) + P(A \cap B_2) + P(A \cap B_3) + \cdots$$
Hemos visto anteriormente que la interesección de dos sucesos dependientes se puede representar como:
$$P(A \cap B) = P(B) \cdot P(A \ \vert \ B)$$
Podemos aplicarlo cuando la variable $B$ puede cumplirse ($B$) o no ($\overline{B}$).
$$\begin{array}{ccccc} P(A) & = & P(A \cap B) & + & P(A \cap \overline{B}) \\ P(A) & = & P(B) \cdot P(A \ \vert \ B) & + & P(\overline{B}) \cdot P(A \ \vert \ \overline{B}) \end{array}$$
De igual forma, podemos aplicarlo cuando desglosamos la variable $B$ en varios subcasos disjuntos.
$$\begin{array}{ccccccc} P(A) & = & P(A \cap B_1) & + & P(A \cap B_2) & + & \cdots \\ P(A) & = & P(B_1) \cdot P(A \ \vert \ B_1) & + & P(B_2) \cdot P(A \ \vert \ B_2) & + & \cdots \end{array}$$
Ejercicios del teorema de probabilidad total
Vamos a realizar un ejercicio que ya resolvimos con el diagrama de árbol:
Ejercicio
Tenemos dos cajas con bolas de colores dentro. La primera caja tiene dos bolas rojas y dos verdes. La segunda caja tiene una bola roja, dos verdes y tres negras.
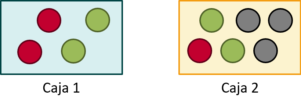
Tiramos una moneda. Si sale cara, elegimos una bola al azar de la primera caja. Si sale cruz, elegimos una bola al azar de la segunda caja. Calcula también la probabilidad de sacar una bola roja.
Solución
Utilizamos el teorema de probabilidad total para desglosar la probabilidad de sacar una bola roja en casos según la caja elegida.
$$P(\textrm{Roja}) = P(\textrm{Roja} \cap \textrm{Caja 1}) + P(\textrm{Roja} \cap \textrm{Caja 2})$$
Utilizamos la fórmula de la intersección de sucesos depedientes:
$$P(\textrm{Roja}) = P(\textrm{Caja 1}) \cdot P(\textrm{Roja} \ \vert \ \textrm{Caja 1}) + P(\textrm{Caja 2}) \cdot P(\textrm{Roja} \ \vert \ \textrm{Caja 2})$$
El enunciado nos proporciona todas estas probabiliades:
- Es igual de probable elegir la caja 1 que la caja 2: $P(\textrm{Caja 1}) = P(\textrm{Caja 2}) = 0,5$.
- En la caja 1, hay 2 bolas roja de 4 en total: $P(\textrm{Roja} \ \vert \ \textrm{Caja 1}) = 2/4$.
- En la caja 2, hay 1 bola roja de 6 en total: $P(\textrm{Roja} \ \vert \ \textrm{Caja 2}) = 1/6$.
Sustituyendo en la fórmula anterior, nos queda:
$$P(\textrm{Roja}) = 0,5 \cdot \dfrac{2}{4} + 0,5 \cdot \dfrac{1}{6} = 0,333$$
Es decir, hay un $33,3\%$ de probabilidades. Lo mismo que nos quedaba con el diagrama de árbol.
Ejercicio
En una fábrica de juguetes hay 3 máquinas ($A$, $B$ y $C$) para fabricarlos. La máquina $A$ fabrica el 70% de los juguetes, la máquina $B$ el 20% y la máquina $C$ el 10% restante.
Sin embargo, estas máquinas también cometen errores durante la fabricación. Un 1% de los juguetes que fabrica la máquina $A$ son defectuosos, por un 2% de la máquina $B$ y un 3% de la máquina $C$.
Calcula la probabilidad de que un juguete sea defectuoso.
Solución
Lo primero que hacemos es traducir el enunciado a lenguaje matemático. Para ello, llamamos $\textrm{Def.}$ al suceso de que un juguete sea defectuoso:
- «La máquina $A$ fabrica el 70% de los juguetes, la máquina $B$ el 20% y la máquina $C$ el 10% restante»: $P(A)=0,7$, $P(B)=0,2$, $P(C)=0,1$
- «Un 1% de los juguetes que fabrica la máquina $A$ son defectuosos, por un 2% de la máquina $B$ y un 3% de la máquina $C$»: $P(\textrm{Def.} \ \vert \ A)=0,01$, $P(\textrm{Def.} \ \vert \ B)=0,02$, $P(\textrm{Def.} \ \vert \ C)=0,03$
- «Calcula la probabilidad de que un juguete sea defectuoso»: $P(\textrm{Def.})$
Aplicamos el teorema de la probabilidad total para desglosar la probabilidad de que sea defectuoso en varios casos en función de la máquina que lo ha realizado:
$$P(\textrm{Def.}) = P(\textrm{Def.} \cap A) + P(\textrm{Def.} \cap B) + P(\textrm{Def.} \cap C)$$
Utilizamos la fórmula de la intersección de sucesos depedientes:
$$P(\textrm{Def.}) = P(A) \cdot P(\textrm{Def.} \ \vert \ A) + P(B) \cdot P(\textrm{Def.} \ \vert \ B) + P(C) \cdot P(\textrm{Def.} \ \vert \ C)$$
Sustituimos los valores de las probabilidades:
$$P(\textrm{Def.}) = 0,7 \cdot 0,01 + 0,2 \cdot 0,02 + 0,1 \cdot 0,03 = 0,012$$
La probabilidad de que un juguete sea defectuoso es de un $1,2\%$.
Para acabar con esta introducción a la probabilidad vamos a ver el teorema o fórmula de Bayes, que mezcla la probabilidad condicionada, la intersección de sucesos dependientes y el teorema de probabilidad total.
