Hemos visto que el espacio muestral ($\Omega$) es la lista de todos los posibles resultados que puede tener un experimento. Por ejemplo, cuando una pareja va a tener un hijo hay dos posibilidades: que sea un niño o que sea una niña. Por lo tanto, su espacio muestral será:
$$\Omega = \{\textrm{un niño, una niña}\}$$
Tenemos dos opciones. Como ambas son igual de probables, gracias a la regla de Laplace podemos afirmar que hay un 50% de posibilidades de que sea un niño y otro 50% de que sea una niña.
Hasta ahí sencillo. Demasiado. Vamos a complicarlo un poco. Ahora vamos a considerar que una pareja tiene dos hijos y no sabemos nada respecto a su sexo. Podríamos decir que hay 3 posibilidades:
$$\Omega = \{\textrm{dos niños, dos niñas, un niño y una niña}\}$$
Al haber 3 posibilidades, ¿significa eso que la probabilidad de cada una de las opciones es de un $33,33\%$? ¡Cuidado! Para poder utilizar la regla de Laplace y repartir las probabilidades a partes iguales entre todas las opciones se tiene que cumplir algo muy importante: todas las opciones tienen que tener la misma probabilidad. Y en este caso no la tienen.
¿Cómo podemos calcular la probabilidad de cada opción? Podemos crear un diagrama de árbol que vaya considerando todo lo que puede pasar con cada hijo. Para el primer hijo hay dos posibilidades: niño o niña. Para no tener que escribir tanto vamos a representar un niño con $O$ y una niña con $A$. El diagrama de árbol muestra las dos opciones con sus probabilidades:
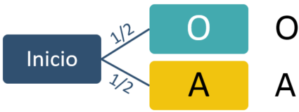
Vamos ahora con el segundo hijo. Para cada resultado del primer hijo, vuelve a haber dos posibilidades para el segundo: niño o niña. El diagrama de árbol muestra todas las opciones y sus probabilidades:
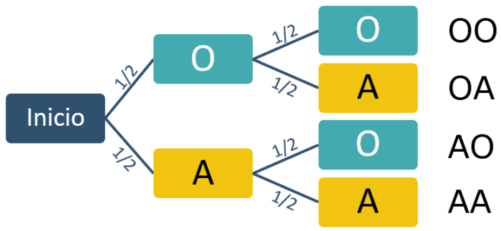
¿Y cómo podemos usar el diagrama de árbol para calcular una probabilidad? Vamos a calcular la probabilidad de que los dos hijos sean niñas. De las cuatro opciones finales, sólo nos vale una ($AA$). Por lo tanto, el primer hijo tiene que ser una niña (probabilidad $1/2$) y el segundo hijo también (probabilidad $1/2$ también). Como se tienen que dar ambas opciones y ambos sucesos son independientes, multiplicamos sus probabilidades.
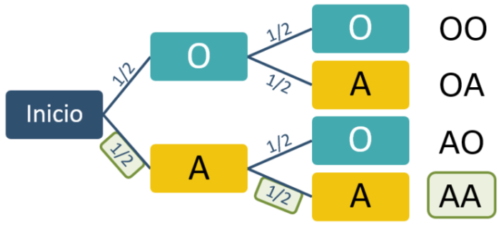
Escribimos la probabilidad del caso $AA$ (que ambos hijos sean niñas) como $P(AA)$:
$$P(AA) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4}$$
Además, en este caso (no ocurrirá siempre) hemos conseguido escribir la lista de resultados posibles como 4 casos igual de probables. Por lo tanto, la probabilidad de cada caso será $1/4$. El espacio muestral queda así:
$$\Omega = \{\textrm{OO, OA, AO, AA}\}$$
¿Cuál sería la probabilidad de que una pareja con dos hijos tenga uno de cada sexo? Hay 2 casos favorables ($OA$ y $AO$) de 4 casos totales. Como todos los casos tienen la misma probabilidad, entonces la probabilidad de que los dos hijos sean de sexos distintos será $2/4$. Es decir, un $50\%$.
Ejercicios de la probabilidad en diagramas de árbol
Prueba a hacer el siguiente ejercicio, un poco más complicado, para comprobar si lo has entendido bien:
Ejercicio
Tenemos dos cajas con bolas de colores dentro. La primera caja tiene dos bolas rojas y dos verdes. La segunda caja tiene una bola roja, dos verdes y tres negras.
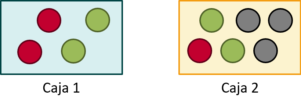
Tiramos una moneda. Si sale cara, elegimos una bola al azar de la primera caja. Si sale cruz, elegimos una bola al azar de la segunda caja.
Utiliza el diagrama de árbol para calcular la probabilidad de elegir una bola negra. Calcula también la probabilidad de sacar una bola roja.
Solución
Dibujamos el diagrama de árbol con todas las opciones y sus probabilidades.
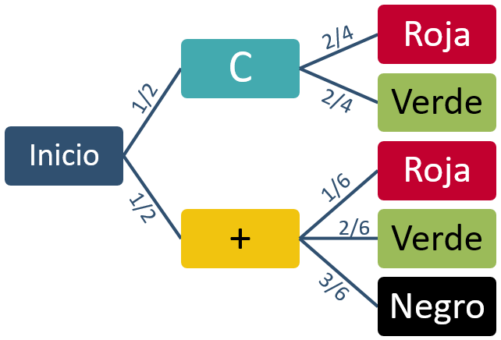
Para que salga una bola negra tiene que salir cruz en la moneda (probabilidad $1/2$) y elegir una bola negra de la segunda caja (probabilidad $3/6$). Multiplicamos las probabilidades:
$$P(\textrm{negra})=\dfrac{1}{2}\cdot\dfrac{3}{6}=\dfrac{1}{4}=0,25=25\%$$
Calculemos ahora la probabilidad de elegir una bola roja. Ahora tenemos dos opciones, ya que hay bolas rojas en ambas cajas. Vamos a calcular la probabilidad de cada opción y después las sumaremos.
$$P(\textrm{roja caja 1})=\dfrac{1}{2}\cdot\dfrac{2}{4}=\dfrac{1}{4}=0,25$$
$$P(\textrm{roja caja 2})=\dfrac{1}{2}\cdot\dfrac{1}{6}=\dfrac{1}{12}=0,083$$
$$P(\textrm{roja})=0,25+0,083=0,333=33,3\%$$
Ahora que ya hemos visto las bases de la teoria de la probabilidad, veamos cuál fue el sorprendente origen de esta disciplina. La probabilidad, tan fundamental en la actualidad, nació casi de casualidad cuando un escritor aficionado a los juegos de azar escribió a dos matemáticos franceses para que le echaran una mano con sus apuestas.
