La función de masa de probabilidad (también conocida como función puntual o función de cuantía) asigna una probabilidad a cada posible valor de la variable aleatoria discreta. Por ejemplo, al tirar 3 monedas, el número de caras puede ser 0, 1, 2 o 3. Podemos ver su diagrama de árbol con los posibles resultados y el número de caras.
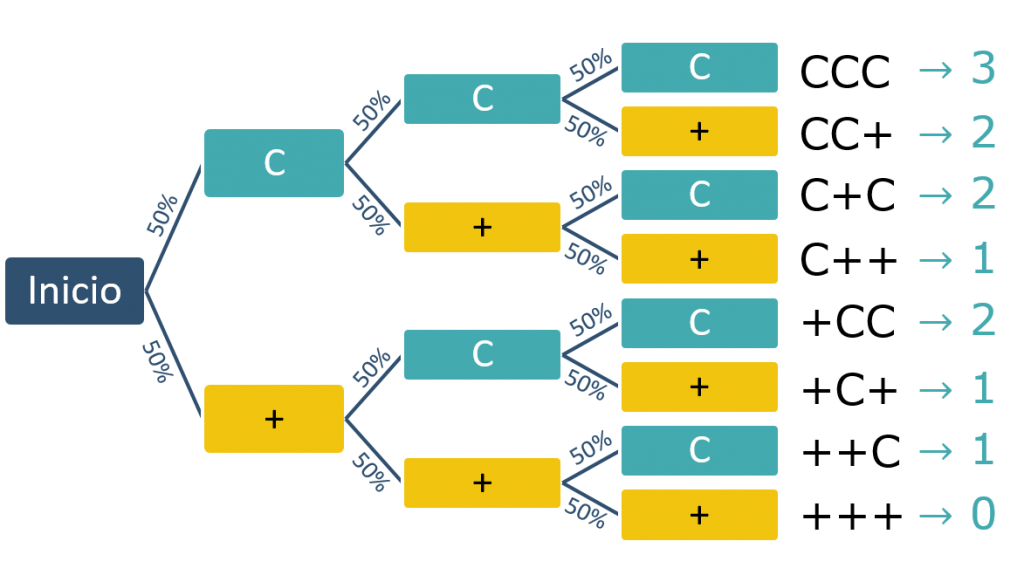
Todos los resultados son igual de probables, con probabilidad $0,125$ ($0,5^3$). Hay un resultado con cero caras, tres con una cara, tres con dos caras y uno con tres caras. La función de masa asigna la probabilidad a cada posible resultado.
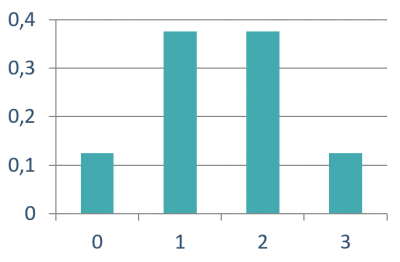
| $x_i$ | $P(\textrm{NumCaras}=x_i)$ |
| 0 | 0,125 |
| 1 | 0,375 |
| 2 | 0,375 |
| 3 | 0,125 |
| 1,000 |
¿Qué probabilidad asigna la función de masa a cualquier otro valor distinto de los listados (0, 1, 2 y 3)? Cero. Por ejemplo, es imposible que el número de caras sea 1,2: $P(\textrm{NumCaras}=1,2)=0$
Podemos observar que hay varias cualidades que una función de masa debe cumplir siempre:
- Las probabilidades asignadas son números entre 0 y 1.
- La suma de todas las probabilidades es siempre 1.
También podemos representar la función de masa gráficamente:
Función de distribución
La función de distribución (también conocida como función de distribución acumulada o función de probabilidad acumulada) se designa con la letra F mayúscula: $F(x)$. En el caso de las monedas, $F(2)$ nos indicará la probabilidad de que el número de caras sea menor o igual que 2. Esta probabilidad incluye tres casos posibles (0, 1 o 2 caras), por lo que sumamos sus probabilidades:
$$\begin{array}{lll}F(2) & = & P(\textrm{NumCaras} \leq 2) \\
& = & P(\textrm{NumCaras}=0) + P(\textrm{NumCaras}=1) + P(\textrm{NumCaras}=2) = 0,875 \end{array}$$
De forma general, tendremos:
$$F(x) = P(\textrm{NumCaras} \leq x)$$
Podemos calcular sus valores realizando el acumulado de la función de masa. Es decir, sumando todos los valores de la función de mesa que tenga por encima en la tabla.
| $x_i$ | $P(\textrm{NumCaras}=x_i)$ | $F(x)$ |
| 0 | 0,125 | 0,125 |
| 1 | 0,375 | 0,500 |
| 2 | 0,375 | 0,875 |
| 3 | 0,125 | 1,000 |
| 1,000 |
¿Qué probabilidad asigna la función de masa a cualquier otro valor distinto de los listados (0, 1, 2 y 3)? Veamos un ejemplo. La probabilidad de que el número de caras sea menor o igual a 1,2 es el mismo que el que sea menor o igual que 1: $F(1.2)=F(1)=0,5$
Por lo tanto, la función de distribución es constante, excepto en aquellos valores a los que la función de masa asigna una probabilidad (0, 1, 2 y 3 en este ejemplo), donde tiene saltos crecientes. Se ve mejor al representar la función de distribución gráficamente.
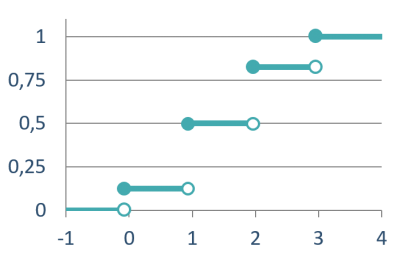
Por lo que podemos definir la función distribución mediante la siguiente fórmula:
$$F(x) = \left\{ \begin{array}{cl} 0 & \textrm{si } x<0 \\ 0,125 & \textrm{si } 0 \leq x < 1 \\ 0,500 & \textrm{si } 1 \leq x < 2 \\ 0,875 & \textrm{si } 2 \leq x < 3 \\ 1,000 & \textrm{si } x \geq 3 \end{array} \right.$$
Podemos observar que hay varias cualidades que posee una función de distribución:
- Toma valores entre 0 y 1.
- La función de distribución tiende a 0 para valores muy pequeños y tiende a 1 para valores muy grandes. Es imposible que el número de caras sea menor o igual a -2, pero es seguro que el número de caras va a ser menor o igual que 500.
Ejercicios de función de masa y de distribución
Ejercicio
Dada la siguiente función de distribución
$$F(x) = \left\{ \begin{array}{cl} 0 & \textrm{si } x<0 \\ 0,25 & \textrm{si } 0 \leq x < 1 \\ 0,4 & \textrm{si } 1 \leq x < 2 \\ 0,68 & \textrm{si } 2 \leq x < 3 \\ 0,9 & \textrm{si } 3 \leq x < 4 \\ 0,97 & \textrm{si } 4 \leq x < 5 \\ 1 & \textrm{si } x \geq 5 \end{array} \right.$$
Calcula la función de masa.
Solución
La función de masa asignará una probabilidad (distinta de cero) a los valores en los que hay un salto en la función de probabilidad. Esos valores son 0, 1, 2, 3, 4 y 5. La probabilidad de cada valor será igual al salto realizado en ese valor.
- En el valor 0 la función de distribución salta de $0$ a $0,25$. El salto es de $0,25$.
- En el valor 1 el salto es de $0,4 – 0,25 = 0,15$.
- En el valor 2 el salto es de $0,68 – 0,4 = 0,28$.
- En el valor 3 el salto es de $0,9 – 0,68 = 0,22$.
- En el valor 4 el salto es de $0,97 – 0,9 = 0,07$.
- Finalmente, en el valor 5 el salto es de $1 – 0,97 = 0,03$.
Por lo tanto, la función de masa es la siguiente:
| $x_i$ | $P(\textrm{NumCaras}=x_i)$ |
| 0 | 0,25 |
| 1 | 0,15 |
| 2 | 0,28 |
| 3 | 0,22 |
| 4 | 0,07 |
| 5 | 0,03 |
| 1,000 |
Una forma de comprobar si nuestra función de masa tiene sentido es viendo que la suma de todas las probabilidades es, efectivamente, 1.
Vamos a ver a continuación cuál sería la media si realizamos el experimento un número elevado de veces (esperanza) y cómo de alejados están los datos respecto a ese valor (varianza y desviación típica).
