Para entender correctamente el teorema de Bayes tenemos que conocer 3 fórmulas que hemos visto anteriormente.
Probabilidad condicionada
Cuando conocemos cierta información, estamos limitando el espacio muestral. Si sabemos que se ha dado el suceso $B$, la probabilidad de que se cumpla el suceso $A$ la escribiremos como $P(A \ \vert \ B)$.
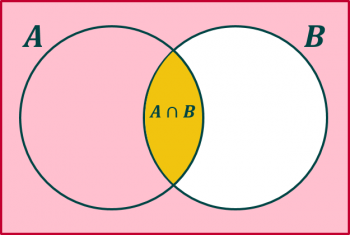
Si se ha dado $B$, estamos seguros de que estamos en el círculo de la derecha. El suceso $A$ se cumplirá si estamos en la parte amarilla. Por lo tanto, la probabilidad que queremos calcular se corresponde con la proporción de amarillo ($A \cap B$) que tiene el círculo de la derecha ($B$).
$$P(A \ \vert \ B) = \dfrac{P(A \cap B)}{P(B)}$$
Ver más sobre probabilidad condicionada.
Intersección de sucesos dependientes
En la fórmula anterior podemos despejar la intersección que hay en el numerador de la fracción.
$$P(A \cap B) = P(B) \cdot P(A \ \vert \ B)$$
Además, como $P(A \cap B) = P(B \cap A)$, obtendremos dos formas de calcular la intersección:
$$P(A \cap B) = \left\{ \begin{array}{c} P(A) \cdot P(B \ \vert \ A) \\ P(B) \cdot P(A \ \vert \ B) \end{array}\right.$$
La probabilidad de que se den dos sucesos es la probabilidad de que se cumpla el primero multiplicada por la probabilidad de que se cumpla el segundo, sabiendo que se ha cumplido el primero.
Ver más sobre intersección de sucesos dependientes.
Teorema de la probabilidad total
Si queremos calcular la probabilidad de un suceso $A$ podemos utilizar otro suceso $B$, que nos dé igual qué valor tome, para desglosar la probabilidad en pequeños casos.
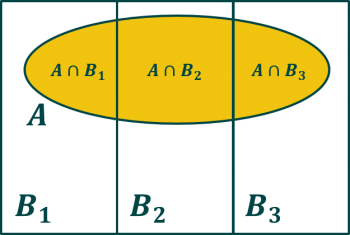
El suceso $A$ se cumple si estamos en la parte amarilla ($A$). que se puede dividir en varias partes (3 en el dibujo).
$$P(A) = P(A \cap B_1) + P(A \cap B_2) + P(A \cap B_3) + \cdots$$
Podemos aplicar la fórmula de la intersección de sucesos independientes (vista arriba) y nos queda:
$$\begin{array}{ccccccc} P(A) & = & P(A \cap B_1) & + & P(A \cap B_2) & + & \cdots \\ P(A) & = & P(B_1) \cdot P(A \ \vert \ B_1) & + & P(B_2) \cdot P(A \ \vert \ B_2) & + & \cdots \end{array}$$
Ver más sobre el teorema de la probabilidad total.
Fórmula de Bayes
La fórmula o regla de Bayes consiste en juntar estas 3 fórmulas que hemos visto arriba. Empezamos con la probabilidad condicionada:
$$P(A \ \vert \ B) = \dfrac{P(A \cap B)}{P(B)}$$
Utilizamos la fórmula de la intersección en el numerador de la fracción:
$$P(A \ \vert \ B) = \dfrac{P(A) \cdot P(B \ \vert \ A)}{P(B)}$$
Por último, aplicamos el teorema de la probabilidad total al denominador de la fracción:
$$P(A \ \vert \ B) = \dfrac{P(A) \cdot P(B \ \vert \ A)}{P(B \cap A_1) + P(B \cap A_2) + P(B \cap A_3) + \cdots}$$
$$P(A \ \vert \ B) = \dfrac{P(A) \cdot P(B \ \vert \ A)}{P(A_1) \cdot P(B \ \vert \ A_1) + P(A_2) \cdot P(B \ \vert \ A_2) + \cdots}$$
Y esta es la fórmula de Bayes. Muchas veces se presenta a los alumnos sin haber visto las otras tres fórmulas, lo que me parece un error. De hecho, si conoces las otras tres fórmulas (más intuitivas que la de Bayes), no tendrás que memorizar el teorema de Bayes.
Ejercicios del teorema de Bayes
Ejercicio
En una fábrica de juguetes hay 3 máquinas ($A$, $B$ y $C$) para fabricarlos. La máquina $A$ fabrica el 70% de los juguetes, la máquina $B$ el 20% y la máquina $C$ el 10% restante.
Sin embargo, estas máquinas también cometen errores durante la fabricación. Un 1% de los juguetes que fabrica la máquina $A$ son defectuosos, por un 2% de la máquina $B$ y un 3% de la máquina $C$.
Se elige un juguete al azar y resulta ser defectuso, ¿cuál es la probabilidad de que sea de la primera máquina $A$?
Solución
Lo primero que hacemos es traducir el enunciado a lenguaje matemático. Para ello, llamamos $\textrm{Def.}$ al suceso de que un juguete sea defectuoso:
- «La máquina $A$ fabrica el 70% de los juguetes, la máquina $B$ el 20% y la máquina $C$ el 10% restante»: $P(A)=0,7$, $P(B)=0,2$, $P(C)=0,1$
- «Un 1% de los juguetes que fabrica la máquina $A$ son defectuosos, por un 2% de la máquina $B$ y un 3% de la máquina $C$»: $P(\textrm{Def.} \ \vert \ A)=0,01$, $P(\textrm{Def.} \ \vert \ B)=0,02$, $P(\textrm{Def.} \ \vert \ C)=0,03$
- «Se elige un juguete al azar y resulta ser defectuso, ¿cuál es la probabilidad de que sea de la primera máquina $A$?»: $P(A \ \vert \ \textrm{Def.})$
Queremos calcular una probabilidad condicionada:
$$P(A \ \vert \ \textrm{Def.}) = \dfrac{P(A \cap \textrm{Def.})}{P(\textrm{Def.})}$$
Empecemos con el numerador. Aplicamos la fórmula de la intersección de sucesos depedientes:
$$P(A \cap \textrm{Def.}) = P(A) \cdot P(\textrm{Def.} \ \vert \ A) = 0,7 \cdot 0,01 = 0,007$$
Vamos ahora con el denominador. Aplicamos el teorema de la probabilidad total para desglosar la probabilidad de que sea defectuoso en varios casos en función de la máquina que lo ha realizado:
$$P(\textrm{Def.}) = P(\textrm{Def.} \cap A) + P(\textrm{Def.} \cap B) + P(\textrm{Def.} \cap C)$$
Utilizamos la fórmula de la intersección de sucesos depedientes:
$$P(\textrm{Def.}) = P(A) \cdot P(\textrm{Def.} \ \vert \ A) + P(B) \cdot P(\textrm{Def.} \ \vert \ B) + P(C) \cdot P(\textrm{Def.} \ \vert \ C)$$
Sustituimos los valores de las probabilidades:
$$P(\textrm{Def.}) = 0,7 \cdot 0,01 + 0,2 \cdot 0,02 + 0,1 \cdot 0,03 = 0,012$$
$$P(A \ \vert \ \textrm{Def.}) = \dfrac{P(A \cap \textrm{Def.})}{P(\textrm{Def.})} = \dfrac{0,007}{0,012} = 0,583$$
Si un juguete es defectuoso, la probabilidad de que haya sido fabricado por la máquina $A$ es de un $58,3\%$.
Una vez terminada esta introducción a la probabilidad, es turno ahora de ser un poco más rigurosos escribiendo y pasar a la probabilidad discreta.
