Hemos visto anteriormente cómo calcular la probabilidad de que ocurran dos sucesos independientes a la vez (intersección de sucesos independientes). Por ejemplo, si lanzo una moneda y un dado al aire y quiero que salga cara en la moneda (probabilidad $1/2$) y un 5 en el dado (probabilidad $1/6$), la probabilidad de que sucedan ambas cosas se calcula multiplicando sus probabilidades, ya que el resultado de uno no influye en el otro (son independientes entre sí):
$$1/2 \cdot 1/6 = 1/12 = 0,083$$
¿Pero qué pasa si los sucesos no son independientes? Veamoslo con un ejemplo.
En una asignatura de la universidad el 80% de los estudiantes asiste regularmente a clase. De entre aquellos que suelen ir a clase, el porcentaje de aprobados es de un 70%, mientras que es de solo un 25% entre aquellos que no asisten a clase. Si elegimos a un estudiante al azar, ¿cuál es la probabilidad de que sea un estudiante que suele asistir a clase y que ha aprobado la asignatura?
Vamos a transformar el enunciado del problema a lenguaje matemático:
- «el 80% de los estudiantes asiste regularmente a clase»: $P(\textrm{Asistir}) = 0,8$
- «De entre aquellos que suelen ir a clase, el porcentaje de aprobados es de un 70%»: $P(\textrm{Aprobar} \ \vert \ \textrm{Asistir}) = 0,7$
- «…mientras que es de solo un 25% entre aquellos que no asisten a clase»: $P(\textrm{Aprobar} \ \vert \ \overline{\textrm{Asistir}}) = 0,25$
- «Si elegimos a un estudiante al azar, ¿cuál es la probabilidad de que sea un estudiante que asiste a clase y que ha aprobado la asignatura?»: $P(\textrm{Asistir} \ \cap \ \textrm{Aprobar})$
Podemos crear un diagrama de árbol para tener una imagen visual del problema:
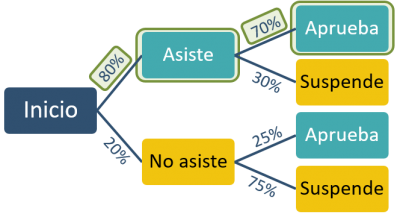
Si buscamos un alumno que asista a clase y que apruebe el examen solo tenemos un camino, por lo que calculamos su probabilidad multiplicando las probabilidades de cada bifurcación.
$$P(\textrm{Asistir} \ \cap \ \textrm{Aprobar}) = 0,8 \cdot 0,7 = 0,56$$
Realmente, si queremos un alumno que asista a clase y que apruebe el examen, necesitamos dos cosas:
- Que asista a clase.
- Que apruebe el examen (sabiendo que asiste a clase).
$$P(\textrm{Asistir} \ \cap \ \textrm{Aprobar}) = P(\textrm{Asistir}) \cdot P(\textrm{Aprobar} \ \vert \ \textrm{Asistir})$$
De forma general tendremos:
$$P(A \cap B) = P(A) \cdot P(B \ \vert \ A)$$
La probabilidad de que se den dos sucesos es la probabilidad de que se cumpla el primero multiplicada por la probabilidad de que se cumpla el segundo, sabiendo que se ha cumplido el primero.
¿Y de dónde viene esta fórmula? Simplemente tenemos que despejar la intersección de la fórmula de la probabilidad condicionada.
$$P(B \ \vert \ A) = \dfrac{P(A \cap B)}{P(A)} \implies P(A \cap B) = P(A) \cdot P(B \ \vert \ A)$$
Por otro lado, como $P(A \cap B) = P(B \cap A)$, obtendremos dos formas de calcular la intersección:
$$P(A \cap B) = \left\{ \begin{array}{c} P(A) \cdot P(B \ \vert \ A) \\ P(B) \cdot P(A \ \vert \ B) \end{array}\right.$$
En nuestro ejemplo habrá dos formas de calcular la intersección. Debemos elegir una u otra según los datos que conozcamos del problema:
$$P(\textrm{Asistir} \cap \textrm{Aprobar}) = \left\{ \begin{array}{c} P(\textrm{Asistir}) \cdot P(\textrm{Aprobar} \ \vert \ \textrm{Asistir}) \\ P(\textrm{Aprobar}) \cdot P(\textrm{Asistir} \ \vert \ \textrm{Aprobar}) \end{array}\right.$$
En este caso hemos calculado la probabilidad de la intersección con la primera forma, ya que conocemos ambas probabilidades.
Propiedades de la intersección de sucesos dependientes
Hemos visto dos fórmulas para calcular la probabilidad de la intersección: para sucesos independientes y para sucesos dependientes. Esta última es la más general, ya que se verifica tanto si los sucesos son dependientes como si no. Por lo tanto, es la que usaremos si desconocemos si hay independencia entre los sucesos.
Cuando dos sucesos son independientes, vimos que uno no influía en el otro:
$$\textrm{Si A y B son independientes} \implies P(B \ \vert \ A) = P(B)$$
Sustituimos en la fórmula general de la intersección:
$$P(A \cap B) = P(A) \cdot P(B \ \vert \ A) = P(A) \cdot P(B)$$
Por lo tanto, obtenemos la fórmula de la intersección para sucesos independientes:
$$\textrm{Si A y B son independientes} \implies P(A \cap B) = P(A) \cdot P(B)$$
Ejercicios de la intersección de sucesos dependientes
Ejercicio
En una baraja francesa hay 52 cartas y 4 palos distintos (corazones, rombos, espadas y picas), por lo que hay 13 cartas de cada palo.
Se saca una carta al azar. Se vuelve a juntar con el resto de cartas y se saca otra carta al azar. Calcula la probabilidad de que ambas cartas sean rombos.
Solución
Como hay 13 cartas de rombos de 52 cartas totales, la probabilidad de la primera carta que hemos sacado sea un rombo es:
$$P(1=\textrm{rombo}) = 13/52 = 0,25$$
Al sacar la primera carta se vuelve a mezclar con el resto de cartas, por lo que estamos ante el mismo escenario que al principio: 52 cartas de las cuales 13 son rombos. Por lo tanto, la probabilidad de que la segunda carta sea rombo también es:
$$P(2=\textrm{rombo}) = 13/52 = 0,25$$
Para calcular la probabilidad de que ambas sean rombos simplemente tenemos que multiplicar sus probabilidades:
$$P(1=\textrm{rombo} \cap 2=\textrm{rombo}) = P(1=\textrm{rombo}) \cdot P(2=\textrm{rombo})$$
$$P(1=\textrm{rombo} \cap 2=\textrm{rombo}) = \dfrac{13}{52} \cdot \dfrac{13}{52} = 0,063 = 6,3\%$$
Ejercicio
En una baraja francesa hay 52 cartas y 4 palos distintos (corazones, rombos, espadas y picas), por lo que hay 13 cartas de cada palo.
Se sacan dos cartas a la vez al azar. Calcula la probabilidad de que ambas cartas sean rombos.
Solución
Puede parecer que el problema es el mismo que el anterior, pero no es así. Ten en cuenta que en el problema anterior la carta seleccionada podía ser la misma las dos veces, ya que tras verla se volvía a mezclar con las demás. Ahora, al seleccionar dos cartas, obviamente tienen que ser distintas.
A pesar de que el problema nos dice que se sacan las dos cartas a la vez, vamos a pensar que sacamos primero una y luego la otra. La probabilidad no debería cambiar. Es como si tiramos dos dados a la vez o primero uno y después otro. Las probabilidades no cambian.
Igual que en el problema anterior, la probabilidad de que la primera carta sea un rombo es $13/52 = 0,25$, ya que hay 13 rombos en 52 cartas.
$$P(1=\textrm{rombo}) = 13/52 = 0,25$$
Sin embargo, a la hora de la probabilidad de que la segunda carta sea también un rombo está condicionada por la carta que se haya sacado antes. De hecho, ahora solo habrá 51 cartas entre las que elegir, de las cuales 12 serán rombos. Por lo que la probabilidad de que la segunda sea un basto sabiendo que la primera también lo era es:
$$P(2=\textrm{rombo} \ \vert \ 1=\textrm{rombo}) = 12/51 = 0,235$$
Por lo tanto, la probabilidad de que ambas cartas sean rombos será:
$$P(1=\textrm{rombo} \cap 2=\textrm{rombo}) = P(1=\textrm{rombo}) \cdot P(2=\textrm{rombo} \ \vert \ 1=\textrm{rombo})$$
$$P(1=\textrm{rombo} \cap 2=\textrm{rombo}) = \dfrac{13}{52} \cdot \dfrac{12}{51} = 0,059 = 5,9\%$$
La probabilidad es distinta que en el problema anterior.
Hemos visto cómo varía la fórmula de la intersección en función de si dos sucesos son dependientes o independientes. Vamos a usar esas diferencias para comprobar si dos sucesos son dependientes o independientes.
