Utilizando la intersección hemos visto cómo calcular la probabilidad de que, al tirar dos dados, en ambos el resultado sea un 5. Necesitábamos que en el primer dado saliese un 5 y en el segundo dado también saliese otro 5.
Pero, ¿qué pasa en el caso en el que nos basta con que uno de los dos sea un 5? Para calcular esta probabilidad utilizaremos la unión. En este caso necesitaremos que en el primer dado salga un 5 o en el segundo dado salga un 5. O en uno, o en otro, o en ambos.
Veamos la diferencia que hay entre la intersección y la unión gráficamente. Si tenemos dos sucesos A y B, la intersección será la parte que tengan en común:
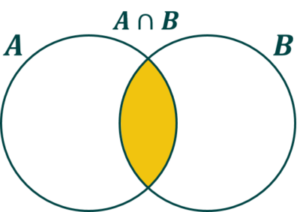
Mientras que la unión será lo que esté en uno, en otro o en los dos:
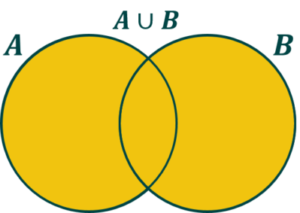
¿Y cómo podemos calcular la probabilidad de la unión de dos sucesos? Veamos qué pasa si sumamos la probabilidad de cada uno por separado. Si sumamos la probabilidad de A y la probabilidad de B, estaríamos contando dos veces la parte que tienen en común (es decir, la intersección). Por lo tanto, tendremos que quitársela una vez. De esta forma:
$$P(A \cup B) = P(A) + P(B) – P(A \cap B)$$
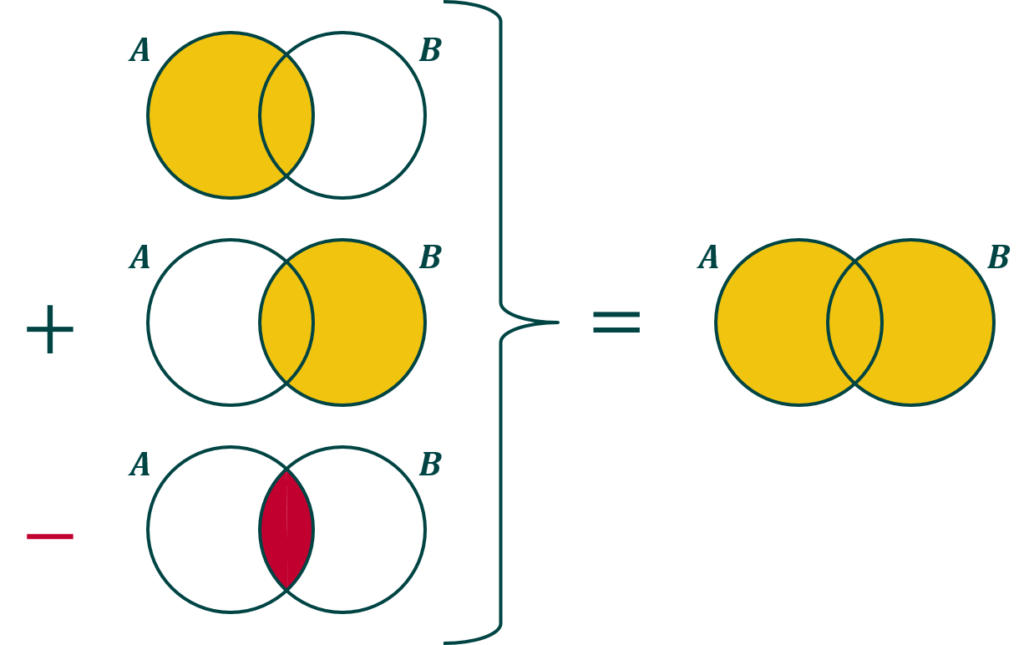
Volvamos al problema de los dados. Tiramos dos dados y queremos que alguno de los dos sea un 5:
$$P(5 \cup 5) = P(5) + P(5) – P(5 \cap 5)$$
La probabilidad de que salga un 5 en cada uno de los dos dados será $1/6$. Por otro lado, la probabilidad de la intersección será la multiplicación de ambas probabilidades, ya que cada el resultado de cada dado es independiente del otro.
$$P(5 \cup 5) = \dfrac{1}{6} + \dfrac{1}{6} – \dfrac{1}{6} \cdot \dfrac{1}{6} = 0,306$$
Por lo tanto, la probabilidad será $0,306$ (es decir, $30,6\%$).
Ejercicios de la probabilidad de la unión
Veamos un ejercicio:
Ejercicio
Tiramos un dado y lanzamos una moneda al aire. Calcula la probabilidad de que salga un 5 en el dado o salga cara en la moneda.
Solución
La probabilidad de que salga un 5 en el dado o salga cara en la moneda es:
$$P(5 \cup \textrm{cara}) = P(5) + P(\textrm{cara}) – P(5 \cap \textrm{cara})$$
La probabilidad de que salga un 5 en el dado es $1/6$. La probabilidad de que salga cara en la moneda es $1/2$. Para calcular la probabilidad de que pasen ambas cosas tenemos que multiplicar sus probabilidades (son sucesos independientes). Por lo tanto, la fórmula anterior nos queda así:
$$P(5 \cup \textrm{cara}) = \dfrac{1}{6} + \dfrac{1}{2} – \dfrac{1}{6} \cdot \dfrac{1}{2} = 0,583$$
La probabilidad de que suceda una de las dos cosas (o ambas) es $0,583$ (es decir, $58,3\%$).
Ya hemos visto cómo calcular la probabilidad de la intersección y de la unión de dos sucesos. Es turno ahora de una idea muy sencilla pero muy poderosa: el suceso contrario.
